Question

Suppose that f:S×S→S is any function. Define gₙ:Sⁿ → S recursively by g₂(x₁,x₂)=f(x₁,x₂), and gₙ₊₁(x₁,x₂,…,xₙ₊₁=f(gn(x₁,x₂,x₃,…,xₙ),xₙ₊₁)

Show that if f is an injection and gₖ is an injection, then gₖ₊₁ is an injection.

Answer 1

If (f) is an injection and (g_k) is an injection, then \
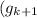`(g_(k+1)\)`is an injection.

Step-by-step explanation:

When a function is an injection, it implies that distinct inputs yield distinct outputs. Assuming \(f\) is an injection implies that for any (x) and (y) in (S, if
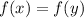`\(f(x) = f(y)\)`, then (x = y). Similarly, if (g_k) is an injection, for any (n)-tuple inputs in \(S^n\), distinct inputs will produce distinct outputs for (g_k).

When
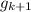`\(g_(k+1)\)`is constructed recursively using (f) and (g_k), the property of
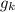`\(g_k\)`being an injection ensures that the inputs fed into \
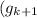`(g_(k+1)\)` are distinct. The function \(f\) being an injection further guarantees that applying (f) to these distinct inputs will result in distinct outputs, maintaining the injection property of
`\(g_(k+1)\).`

Therefore, the combination of \(f\) being an injection and (g_k) being an injection guarantees that
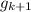`\(g_(k+1)\)`maintains the injection property, ensuring that distinct inputs to
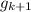`\(g_(k+1)\)`yield distinct outputs.

"".