Question

Let (v1, V2, v3] be a set of nonzero vectors in Rm such that v/ v,0 when i j. Show that the set is linearly independent. [Hint: Set aivi a2V2 + a3V3 and consider el0.] If the set (vi, V2, V3 of vectors in R is linearly 50.

Answer 1

To show that the set of vectors (v1, v2, v3) is linearly independent, we can use the fact that the zero vector can be expressed as a linear combination of the given vectors. By comparing the coefficients, we can conclude that the set of vectors is linearly independent.

Step-by-step explanation:

To show that the set of vectors (v1, v2, v3) is linearly independent, we need to show that the only solution to the equation
`a1*v1 + a2*v2 + a3*v3 = 0 is a1 = a2 = a3 = 0`

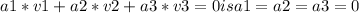
We can use the hint provided in the question, which suggests considering the vector v0 = 0*v1 + 0*v2 + 0*v3. Since the zero vector can be expressed as a linear combination of the given vectors, we can write v0 = a1*v1 + a2*v2 + a3*v3.

By comparing the coefficients, we can conclude that a1 = a2 = a3 = 0. This implies that the set of vectors (v1, v2, v3) is linearly independent.