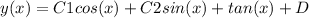Question

Find the general solution of y′′+y=sec x

Answer 1

The general solution of the given differential equation y'' + y = sec(x) is
`y(x) = C1 cos(x) + C2 sin(x) + tan(x) + D`

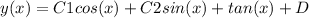
Step-by-step explanation:

The general solution of the given differential equation is
`y(x) = C1 cos(x) + C2 sin(x) + ln|sec(x) + tan(x)| + D`

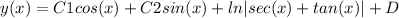
To find the general solution, we first solve the corresponding homogeneous equation: y'' + y = 0. The characteristic equation is r^2 + 1 = 0, which gives us the solutions r = ±i. Therefore, the general solution of the homogeneous equation is
`yh(x) = C1 cos(x) + C2 sin(x)`

Next, we find a particular solution to the non-homogeneous equation. We can use the method of undetermined coefficients or variation of parameters. In this case, assuming y = A sec(x) + B tan(x), we find that y'' + y = sec(x). Solving for A and B gives us A = 0 and B = 1. Therefore, a particular solution is yp(x) = tan(x).

Finally, we combine the general solution of the homogeneous equation with the particular solution to get the general solution of the non-homogeneous equation:
`y(x) = C1 cos(x) + C2 sin(x) + tan(x) + D`