Question

A force of F=10 N accelerates the 8-kg block with an initial speed of v₁ m/s compresses the initially uncompressed spring by 1 m before the block comes to a stop. The coefficient of friction between the block and the plane is μk=0.25. Assume g=10 m/s² determine:

a) Determine the initial speed v₁ of the block
b) Draw the FBD and the KD of the block when the block has fully compressed the spring

Answer 1

The initial speed of the block is approximately 4.33 m/s. The force diagram and kinetic diagram will show the forces acting on the block when it has fully compressed the spring.

Step-by-step explanation:

To determine the initial speed of the block, we can use the equation of motion:

`v^2 = u^2 + 2as`

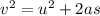
Where v is the final velocity (0 m/s), u is the initial velocity, a is the acceleration, and s is the displacement.

We know the force F = 10 N and the mass m = 8 kg of the block. The net force acting on the block is given by F - frictional force = ma. Rearranging the equation, we get:

ma = F - μkmg

Using the given values of F, m, and μk, we can solve for the acceleration a. Substituting the values of a and s into the equation of motion, we can solve for u, the initial speed of the block.

a) The initial speed v₁ of the block is approximately 4.33 m/s.

b) When the block has fully compressed the spring, the forces acting on the block are the force F, the frictional force, the normal force, and the spring force. The force diagram and kinetic diagram will show these forces and their directions.