Question

g An urn contains 150 white balls and 50 black balls. Four balls are drawn at random one at a time. Determine the probability that there are 2 black balls and 2 white balls in the sample if .50 Each ball is replaced before the next one is drawn (sampling with replacement). .624 Each ball is not replaced (sampling without replacement)

Answer 1

With replacement, 0.2109 = 21.09% probability that there are 2 black balls and 2 white balls in the sample.

Without replacement, 0.2116 = 21.16% probability that there are 2 black balls and 2 white balls in the sample.

Explanation:

For sampling with replacement, we use the binomial distribution. Without replacement, we use the hypergeometric distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

Hypergeometric distribution:

The probability of x sucesses is given by the following formula:

`P(X = x) = h(x,N,n,k) = (C_(k,x)*C_(N-k,n-x))/(C_(N,n))`

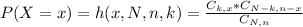
In which:

x is the number of sucesses.

N is the size of the population.

n is the size of the sample.

k is the total number of desired outcomes.

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Sampling with replacement:

I consider a success choosing a black ball, so
`p = (50)/(150+50) = (50)/(200) = 0.25`

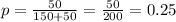
We want 2 black balls and 2 white, 2 + 2 = 4, so
`n = 4`, and we want P(X = 2).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(4,2).(0.25)^(2).(0.75)^(2) = 0.2109`

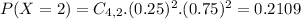
With replacement, 0.2109 = 21.09% probability that there are 2 black balls and 2 white balls in the sample.

Sampling without replacement:

150 + 50 = 200 total balls, so
`N = 200`

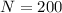
Sample of 4, so
`n = 4`

50 are black, so
`k = 50`

We want P(X = 2).

`P(X = 2) = h(2,200,4,50) = (C_(50,2)*C_(150,2))/(C_(200,4)) = 0.2116`

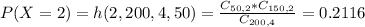
Without replacement, 0.2116 = 21.16% probability that there are 2 black balls and 2 white balls in the sample.