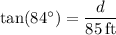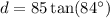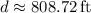Answer:
808.72 ft
Explanation:
We can create a right triangle with the following points:
- the top of the lighthouse
- the base of the lighthouse
- the rock jutting out of the water
I will label the distance from the base of the lighthouse to the rock d.
See the attached image for a detailed model.
Then, solve for the two acute angles of the triangle.
The larger acute angle (∠1) is complementary to 6°, so we can solve by setting their sum to 90°:
6° + m∠1 = 90°
m∠1 = 84°
Because this is a right triangle, the smaller acute angle (∠2) is complementary to the larger acute angle, so we can solve once again by setting their sum to 90°:
m∠1 + m∠2 = 90°
84° + m∠2 = 90°
m∠2 = 6°
We can use either of these angles in combination with the trigonometric ratio tangent to solve for the distance d. I will use tangent of ∠1.