Question

he selected a random sample of 46 men and found that the average number of dress shirts that they owned was 14.7

Answer 1

a) Stating the hypotheses and identifying the claim are as follows:

The null hypothesis
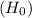`(H_0)`: The average number of dress shirts a man owns has not changed and is still 15.

The alternative hypothesis
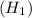`(H_1)`: The average number has changed. The claim is that the average has changed.

b) The computed test value is approximately -1.02.

c) The P-value is 0.3124.

d) Since the P-value (0.3124) is greater than the significance level (α = 0.01), we fail to reject the null hypothesis.

e) The sample data does not provide significant evidence to conclude that the average has changed from the previous study.

a) Hypotheses:

`(H_0: \mu = 15)`

`(H_1: \mu \\eq 15) (Claim)`

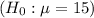
b) Computing the test value:

We can use the formula for the test statistic in a hypothesis test for a population mean:

`(Z = \frac{\bar{X} - \mu}{\sigma / √(n)})`

where:

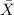`\bar{X}` is the sample mean,

`\mu` is the population mean,

`\sigma` is the population standard deviation, and

n is the sample size.

`(Z = (14.7 - 15)/(2 / √(46)))`

=
`\frac{{-0.3}}{{0.294}}`

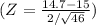
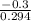
`\approx` -1.02

c) The P-value can be found using the z-table. Since the alternative hypothesis is two-tailed, we look for the probability of z being less than -1.02 and the probability of z being greater than 1.02.

From the z-table, the probability of z being less than -1.02 is approximately 0.1562, and the probability of z being greater than 1.02 is also approximately 0.1562.

The P-value is the sum of these two probabilities: P = 2 * 0.1562 = 0.3124

d) Since the P-value (0.3124) is greater than the significance level (α = 0.01), we fail to reject the null hypothesis.

e) Based on the analysis, there is not enough evidence to support the claim that the average number of dress shirts owned by men has changed.

Complete Question:

Dress Shirts In a previous study conducted several years ago, a man owned on average 15 dress shirts. The standard deviation of the population is 2. A researcher wishes to see if that average has changed. He selected a random sample of 46 men and found that the average number of dress shirts that they owned was 14.7. At α = 0.01, is there enough evidence to support the claim that the average has changed? Assume that the variable is normally distributed. Use the P-value method with a table.

(a) State the hypotheses and identify the claim.

(b) Compute the test value.

(c) Find the P -value.

(d) Make the decision.

(e) Summarize the results.