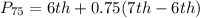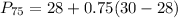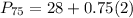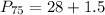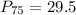Answer:
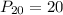 --- 20th percentile
--- 20th percentile
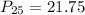 --- 25th percentile
--- 25th percentile
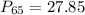 --- 65th percentile
--- 65th percentile
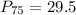 --- 75th percentile
--- 75th percentile
Explanation:
Given
27, 24, 21, 16, 30, 33, 28, and 24.
N = 8
First, arrange the data in ascending order:
Arranged data: 16, 21, 24, 24, 27, 28, 30, 33
Solving (a): The 20th percentile
This is calculated as:
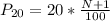
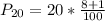
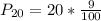
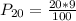
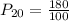
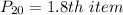
This is then calculated as:
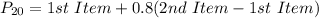
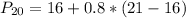
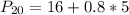
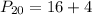
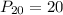
Solving (b): The 25th percentile
This is calculated as:
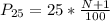
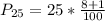
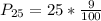
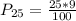
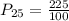
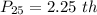
This is then calculated as:
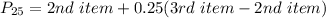
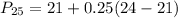
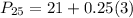
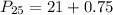
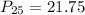
Solving (c): The 65th percentile
This is calculated as:
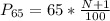
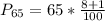
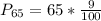
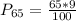
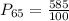
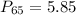
This is then calculated as:
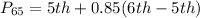
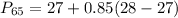
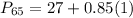
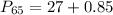
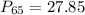
Solving (d): The 75th percentile
This is calculated as:
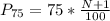
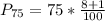
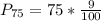
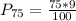
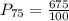
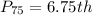
This is then calculated as: