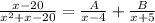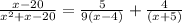Answer:
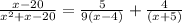
Explanation:
Given
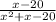
Required
Decompose into partial fraction
Start by factorizing the denominator:
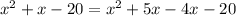
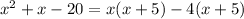
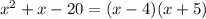
So, we have:
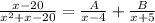
Take LCM
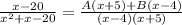
Cancel out the denominator

Open brackets
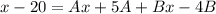
Collect Like Terms
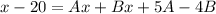
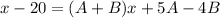
By comparison;
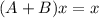 ==>
==>

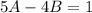
Make A the subject in

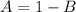
Substitute 1 - B for A in
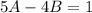


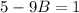
Collect Like Terms
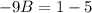
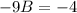
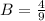
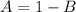
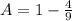
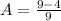
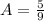
So: