The equation simplifies to
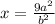 . Therefore, the correct statement is
. Therefore, the correct statement is
 when the expression
when the expression
 holds true.
holds true.
Let's analyze the given equation and the options:
![\[ (x)/(y) / (3a)/(b) = (3a)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/dqdgjdnezi9mst0igly6b8hmq2ll2ejvpz.png)
To solve this, we can simplify the expression on the left by multiplying by the reciprocal of the divisor:
![\[ (x)/(y) * (b)/(3a) = (3a)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/llx2k1lvehgwvtx7t3ntbq40vnkroygx0i.png)
Now, simplify:
![\[ (xb)/(3ay) = (3a)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/ka6rznbov0t4lvmzy4clrw1d0uiu3nilo6.png)
To isolate x, multiply both sides by
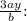
![\[ xb = ((3a)^2)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/48ogetq1k5ntty99qzmwtjdhnyxw2m0jyh.png)
![\[ xb = (9a^2)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/d2dx84u0oaxy2ejw3josf0hk51ftgex7dz.png)
Now, divide both sides by b:
![\[ x = (9a^2)/(b^2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/r052aq5v4hv1s6gjm4avw4y2oxwjboxmls.png)
So, the correct option is:
![\[ (x)/(y) = (9a^2)/(b^2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/q0cqcwf1how2vmss3gbhbjojs6bunmkpf9.png)
The probable question may be:
What must be true if (x)/(y)-:(3a)/(b)=(3a)/(b) ? Assume a!=0,b!=0, and y!=0. x=y x=0 (x)/(y)=(b^(2))/(9a^(2)) (x)/(y)=(9a^(2))/(b^(2))