Question

An aluminum wire having a cross-sectional area equal to 2.20 10-6 m2 carries a current of 4.50 A. The density of aluminum is 2.70 g/cm3. Assume each aluminum atom supplies one conduction electron per atom. Find the drift speed of the electrons in the wire.

Answer 1

The drift speed of the electrons in the wire is 2.12x10⁻⁴ m/s.

Step-by-step explanation:

We can find the drift speed by using the following equation:

`v = (I)/(nqA)`

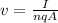
Where:

I: is the current = 4.50 A

n: is the number of electrons

q: is the modulus of the electron's charge = 1.6x10⁻¹⁹ C

A: is the cross-sectional area = 2.20x10⁻⁶ m²

We need to find the number of electrons:

`n = (6.022\cdot 10^(23) atoms)/(1 mol)*(1 mol)/(26.982 g)*(2.70 g)/(1 cm^(3))*((100 cm)^(3))/(1 m^(3)) = 6.03 \cdot 10^(28) atom/m^(3)`

Now, we can find the drift speed:

`v = (I)/(nqA) = (4.50 A)/(6.03 \cdot 10^(28) atom/m^(3)*1.6 \cdot 10^(-19) C*2.20 \cdot 10^(-6) m^(2)) = 2.12 \cdot 10^(-4) m/s`

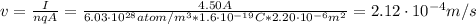
Therefore, the drift speed of the electrons in the wire is 2.12x10⁻⁴ m/s.

I hope it helps you!