Question

Suppose the following tables present the number of specimens that tested positive for Type A and Type B influenza in a country during a flu season. Type A 38 100 186 199 253 380 595 966 1611 2638 3845 4931 5183 5367 5890 Type B 59 95 116 143 156 225 271 366 495 696 851 1060 1140 1101 1202 Send data to Excel (a) Find the mean and median number of Type A cases. Round the answers to at least one decimal place. (b) Find the mean and median number of Type B cases. Round the answers to at least one decimal place. (c) A public health official says that there are more than twice as many cases of Type A influenza than Type B. Do these data support this claim

Answer 1

(a) Mean and Median of type A

`\bar x = 2145.47`

`Median = 966`

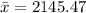
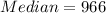
(b) Mean and Median of type B

`\bar x = 531.73`

`Median = 366`

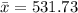
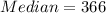
(c) The claim by the public health worker is true.

Explanation:

Given

`Type\ A: 38\ 100\ 186\ 199\ 253\ 380\ 595\ 966\ 1611\ 2638\ 3845\ 4931\ 5183\ 5367\ 5890`

`Type\ B: 59\ 95\ 116\ 143\ 156\ 225\ 271\ 366\ 495\ 696\ 851\ 1060\ 1140\ 1101\ 1202`

`n = 15`

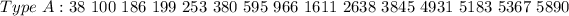
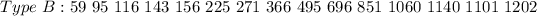
Solving (a): The mean and median of A.

Mean is calculated using:

`\bar x = (\sum x)/(n)`

`\bar x = (38 +100 +186 +199+ 253+ 380+ 595+ 966 +1611 +2638 +3845+ 4931+ 5183 +5367 +5890 )/(15)`

`\bar x = (32182)/(15)`

`\bar x = 2145.47`

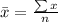
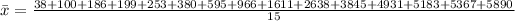
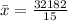
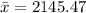
The median is calculated using:

`Median = (n+1)/(2)th`

`Median = (15+1)/(2)th`

`Median = (16)/(2)th`

`Median = 8th`

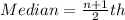
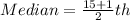
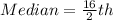
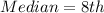
The 8th item is: 966

So:

`Median = 966`

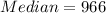
Solving (b): The mean and median of B.

Mean is calculated using:

`\bar x = (\sum x)/(n)`

`\bar x = (59 +95 +116+ 143+ 156+ 225+ 271+ 366+ 495 +696+ 851+ 1060+ 1140 +1101+ 1202)/(15)`

`\bar x = (7976)/(15)`

`\bar x = 531.73`

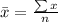
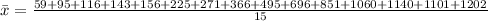
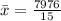
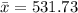
The median is calculated using:

`Median = (n+1)/(2)th`

`Median = (15+1)/(2)th`

`Median = (16)/(2)th`

`Median = 8th`

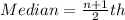
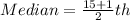
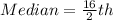
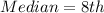
The 8th item is: 366

So:

`Median = 366`

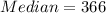
(c) The claim by the public health worker is true.

To do this, we simply compare the mean value of both types.

For Type A

`\bar x = 2145.47`

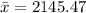
For Type B

`\bar x = 531.73`

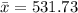
The claim is:

`Type\ A > 2 * Type B`

`2145.47 > 2 * 531.73`

`2145.47 > 1063.46`

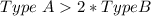
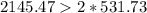
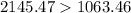
Since the inequality is true, then the claim is true