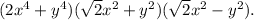The expression
 is factored into
is factored into
 using the sum of cubes identity and the difference of two squares.
using the sum of cubes identity and the difference of two squares.
The expression
 cannot be factored into simple linear or quadratic factors. However, we can decompose it using the sum of cubes identity,
cannot be factored into simple linear or quadratic factors. However, we can decompose it using the sum of cubes identity,
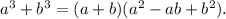
By applying this identity, we consider
 as
as
 and
and
 . The expression becomes:
. The expression becomes:
![\[ (2x^4)^2 + (y^4)^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/3ab8r4fk76ykxwyxmxh8yk9z2ikt3a43x4.png)
Now, we apply the sum of two squares identity:
![\[ (2x^4 + y^4)(2x^4 - y^4) \]](https://img.qammunity.org/2024/formulas/mathematics/college/cot1n1c6gz8j483bi4ddlo7krzd2v8o80n.png)
Inside the parentheses,
 cannot be factored further, but
cannot be factored further, but
 can be decomposed as the difference of two squares:
can be decomposed as the difference of two squares:
![\[ (2x^4 + y^4)(√(2)x^2 + y^2)(√(2)x^2 - y^2) \]](https://img.qammunity.org/2024/formulas/mathematics/college/eshdb7fxv7kx263mo1fsz4pnn9dqbavk3e.png)
Therefore, the original expression
 can be factored into
can be factored into