Answer:
0.3333 = 33.33% of this group likes chocolate
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
Of the friends who like sprinkles, what proportion of this group likes chocolate:
So,
Event A: Likes sprinkles
Event B: Likes chocolate
15% of your friends like sprinkles (S) topping.
This means that
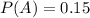
5% of your friends like Chocolate (C) and also like sprinkles (S).
This means that
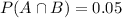
So
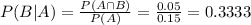
0.3333 = 33.33% of this group likes chocolate