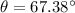The ladder makes 75.43 degrees with the wall and the ground. To the nearest degree, the support wire makes 67 degrees with the pole and the ground.
Problem 2: A ladder leans against a wall
Let's denote the following:
-
 : height on the wall the ladder reaches (15 feet)
: height on the wall the ladder reaches (15 feet)
-
 : distance from the base of the ladder to the wall (3.9 feet)
: distance from the base of the ladder to the wall (3.9 feet)
-
 : the angle the ladder makes with the wall and the ground
: the angle the ladder makes with the wall and the ground
Using trigonometry, specifically the tangent function, we can set up the following equation:
![\[ \tan(\theta) = (h)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/8o2now4t63pmvn7qlgkr4gr12eh06g9og7.png)
Substitute the given values:
![\[ \tan(\theta) = (15)/(3.9) \]](https://img.qammunity.org/2024/formulas/mathematics/college/tzlflstsa3xw4jhka5uly6vw4bm34l1fb0.png)
Now, you can find
 by taking the arctangent (inverse tangent) of both sides:
by taking the arctangent (inverse tangent) of both sides:
![\[ \theta = \tan^(-1)\left((15)/(3.9)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/pch1xq6v2c730h0jvyvyet8wcvln911ril.png)
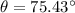
Problem 3: A support wire from a utility pole
Let's denote:
-
 : height on the pole the wire reaches (7.2 meters)
: height on the pole the wire reaches (7.2 meters)
-
 : distance from the base of the pole to the point on the ground (3 meters)
: distance from the base of the pole to the point on the ground (3 meters)
-
 : the angle the wire makes with the pole and the ground
: the angle the wire makes with the pole and the ground
Again, using trigonometry and the tangent function:
![\[ \tan(\theta) = (h)/(b) \]](https://img.qammunity.org/2024/formulas/mathematics/college/8o2now4t63pmvn7qlgkr4gr12eh06g9og7.png)
Substitute the given values:
![\[ \tan(\theta) = (7.2)/(3) \]](https://img.qammunity.org/2024/formulas/mathematics/college/mstwwx17p6rpgty2w8ln79bwzo0t8khfc7.png)
Now, find
 by taking the arctangent of both sides:
by taking the arctangent of both sides:
![\[ \theta = \tan^(-1)\left((7.2)/(3)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/459el553xiarzuj6jug36b0j3qmezz38ub.png)