Question

An advertising agency notices that approximately 2 in 50 potential buyers of a product sees a given magazine ad, and 1 in 7 sees a corresponding ad on television. One in 100 sees both. One in 5 actually purchases the product after seeing the ad, 1 in 10 without seeing it. What is the probability that a randomly selected potential customer will purchase the product

Answer 1

the probability that a randomly selected potential customer will purchase the product is 0.11728

Explanation:

Given the data in the question;

by hypothesis, let the event be given as;

M = buyers sees a given magazine ad of the product

T = buyers sees a given television ad of the product

`P_(A)` = buyer purchases the product after seeing the ad

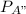`P_(A` = buyer purchase the product without seeing the ad

from the information given in the question;

P(M) = (2/50 ) = 0.04, P(T) = ( 1/7) = 0.1428, P(M∩T) = (1/100) = 0.01,

P(
`P_(A)`) = (1/5) = 0.2, p(
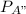`P_(A` ) = (1/10) = 0.1

now, the probability that the buyer sees the ad of the product will be;

P( M ∪ T ) = P( M) + P(T) - p( M ∩ T)

P( M ∪ T ) = 0.04 + 0.1428 - 0.01

P( M ∪ T ) = 0.1728

The probability that the buyer does not see the ad of the product will be;

P( M ∪ T )' = 1 - P( M ∪ T )

= 1 - 0.1728

= 0.8272

Now, the probability that a randomly selected potential customer will purchase the product will be;

P(P) = P(
`P_(A)`) P( M ∪ T ) + p(
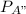`P_(A` )P( M ∪ T )'

P(P) = (0.2)(0.1728) + (0.1)(0.8272)

= 0.03456 + 0.08272

P(P) = 0.11728

Therefore, the probability that a randomly selected potential customer will purchase the product is 0.11728