Answer:
21/72 = 0.2917 = 29.17% probability that a 6 is rolled both times
Explanation:
Two have faces numbered 1,2,3,4,5, and 6
So for these two, each with 1/4 probability of being chosen, the probability of rolling two six is given by:
(1/6)^2 = 1/36
So
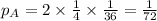
One has faces numbered 2,2,4,4, 6 and 6;
The probability of rolling 2 faces six with this dice is:
(2/6)^2 = 4/36
This dice has 1/4 probability of being chosen. So

One has all six faces numbered 6.
The probabilityu of rolling two six is given by:
(6/6)^2 = 1^2 = 1
This dice has 1/4 probability of being chosen. So
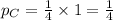
Calculate the probability that a 6 is rolled both times
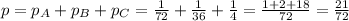
21/72 = 0.2917 = 29.17% probability that a 6 is rolled both times