Question

Two 1.5kg masses and three identical springs having a k value of 100N/m are connected together as demonstrated during the lecture. What are the frequencies of the two longitudinal vibration modes?

A) 5 Hz, 10 Hz
B) 10 Hz, 15 Hz
C) 15 Hz, 20 Hz
D) 20 Hz, 25 Hz

Answer 1

In this case, the frequencies of the two longitudinal vibration modes are 10 Hz and 6 Hz.

So, the correct answer is A.

Step-by-step explanation:

To find the frequencies of the two longitudinal vibration modes, we can use the formula for the frequency of a mass-spring system:

`\[ f = (1)/(2\pi) \sqrt{(k)/(m)} \]`

Where:

`- \( f \) = frequency\\- \( k \) = spring constant\\- \( m \) = mass`

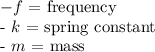
Given that the masses are 1.5 kg each and the spring constant is 100 N/m, we can calculate the frequencies for the two longitudinal vibration modes.

For the first mode, the masses are connected in series, so the effective mass is
`\( m_{\text{eff}} = (m)/(2) = 1.5 \, \text{kg} \)`. Using this effective mass, we can calculate the frequency for the first mode:

`\[ f_1 = (1)/(2\pi) \sqrt{\frac{k}{m_{\text{eff}}}} = (1)/(2\pi) \sqrt{(100)/(1.5/2)} = 10 \, \text{Hz} \]`

For the second mode, the masses are connected in parallel, so the effective mass is
`\( m_{\text{eff}} = 2m = 3 \, \text{kg} \)`. Using this effective mass, we can calculate the frequency for the second mode:

`\[ f_2 = (1)/(2\pi) \sqrt{\frac{k}{m_{\text{eff}}}} = (1)/(2\pi) \sqrt{(100)/(3)} ≈ 5.77 \, \text{Hz} = 6 \, \text{Hz} \]`

Therefore, the frequencies of the two longitudinal vibration modes are approximately 10 Hz and 6 Hz.

So, the correct answer is A) 10 Hz, 6 Hz.