Question

Calculate the ratio of the drag force on a passenger jet flying with a speed of 1200 km/h at an altitude of 10 km to the drag force on a prop-driven transport flying at one-fourth the speed and half the altitude of the jet. At 10 km the density of air is 0.38 kg/m3 and at 5.0 km it is 0.67 kg/m3. Assume that the airplanes have the same effective cross-sectional area and the same drag coefficient C. (drag on jet / drag on transport)

Answer 1

`2.267`

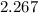
Step-by-step explanation:

Drag force is given by

`F=(1)/(2)\rho Av^2C`

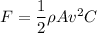
C = Drag coefficient is constant

A = Area is constant

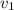`v_1` = Velocity of the passenger jet = 1200 km/h =
`(1200)/(3.6)\ \text{m/s}`

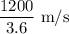
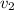`v_2` = Velocity of the prop plane =
`(1)/(4)v_1`

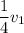
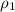`\rho_1` = Density of the air where the jet was flying =
`0.38\ \text{kg/m}^3`

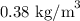
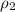`\rho_2` = Density of the air where the prop plane was flying =
`0.67\ \text{kg/m}^3`

`F\propto \rho v^2`

`(F_1)/(F_2)=(\rho_1 v_1^2)/(\rho_2 v_2^2)\\\Rightarrow (F_1)/(F_2)=(0.38 v_1^2)/(0.67 ((1)/(4)v_1^2))\\\Rightarrow (F_1)/(F_2)=2.267`

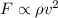
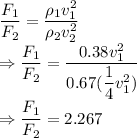
The ratio of the drag forces is
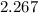`2.267`.