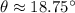In a right-angled triangle with a hypotenuse of 12 and angle A denoted as θ, calculations yield tan(37°) ≈ 1.1314. For cos(θ) = 0.2376, solving yields θ ≈ 18.75°.
Let's use the given information to find the values of the trigonometric ratios.
Given a right-angled triangle ABC with hypotenuse h = 12, and angle A denoted by
 , we can use the Pythagorean theorem to find the length of the adjacent side (base), denoted as b. The Pythagorean theorem is given by:
, we can use the Pythagorean theorem to find the length of the adjacent side (base), denoted as b. The Pythagorean theorem is given by:
![\[ a^2 + b^2 = h^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/wh1mc5np91bs11gc74mhtu50z0aknwz6px.png)
For this triangle:
![\[ a^2 + b^2 = 9^2 + b^2 = 12^2 \]](https://img.qammunity.org/2024/formulas/mathematics/college/39v9s3f40wp1sj5jdrgzmdsbhhwbl6mi38.png)
![\[ 81 + b^2 = 144 \]](https://img.qammunity.org/2024/formulas/mathematics/college/swivaaiw9p022bw4apnv9hrrpu62nx2ogm.png)
![\[ b^2 = 63 \]](https://img.qammunity.org/2024/formulas/mathematics/college/xhxavxjrnt7hpxt8krjj7kvlj6r1guxtby.png)
![\[ b = √(63) \]](https://img.qammunity.org/2024/formulas/mathematics/college/2d5ju8g2s5pl9jzobsoeiybzyn6r4oy3ue.png)
Now, we can use these values to find the trigonometric ratios:
a)
![\[ \tan \theta = (a)/(b) = (9)/(√(63)) \approx 1.1314 \]](https://img.qammunity.org/2024/formulas/mathematics/college/urpdr45e7glkk1u54a1qma0tcil9ga2sn4.png)
b) Given
 , we can use the fact that
, we can use the fact that
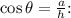
![\[ 0.2376 = (√(63))/(12) \cos \theta \]](https://img.qammunity.org/2024/formulas/mathematics/college/ba7ljwfmf6c3fy4bbg9hsn6rr6p7coe7hn.png)
Solving for
![\[ \theta = \cos^(-1) \left( (0.2376 \cdot 12)/(√(63)) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/hcbpckx7744ia8n3j79fqrhhlafez9di53.png)
![\[ \theta \approx \cos^(-1)(0.9504) \]](https://img.qammunity.org/2024/formulas/mathematics/college/2z7si1h6ak5qjnfgfo3itl397upsmgxbwn.png)
![\[ \theta \approx 18.75^\circ \]](https://img.qammunity.org/2024/formulas/mathematics/college/ofymovg6q9wpeotwdamcheogssa1p4iiei.png)
Summary:
a)
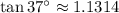
b)