Answer:
a) The standard deviation of this sampling distribution is 2.07.
b) The missing number is 4.14.
c) The 95% confidence interval for the population mean score μ based on this one sample is between 267.86 and 276.14.
Explanation:
To solve this question, we need to understand the Empirical Rule and the Central Limit Theorem.
Empirical Rule:
The Empirical Rule states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
Central Limit Theorem:
The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
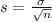 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
In this question:
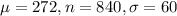
(a) If we take many samples, the sample mean x⎯⎯⎯ varies from sample to sample according to a Normal distribution with mean equal to the unknown mean score μ in the population. What is the standard deviation of this sampling distribution?
Using the Central Limit Theorem:
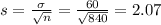
The standard deviation of this sampling distribution is 2.07.
(b) According to the 95 part of the 68-95-99.7 rule, 95% of all values of x⎯⎯⎯ fall within _______ on either side of the unknown mean μ. What is the missing number?
Within 2 standard deviations of the mean.
So, 2*2.07 = 4.14
The missing number is 4.14.
(c) What is the 95% confidence interval for the population mean score μ based on this one sample?
Within 4.14 of the mean
272 - 4.14 = 267.86
272 + 4.14 = 276.14
The 95% confidence interval for the population mean score μ based on this one sample is between 267.86 and 276.14.