Question

Describe and graph all numbers that satisfy both inequalities. $\frac{n}{3}\ge-4$ and $\frac{n}{-5}\ge1$

Answer 1

The solution set of the compound inequality that satisfies both inequalities is -12 ≤ n ≤ -5.

The graph of compound inequalities on number line.

To describe the graph of the compound inequality
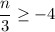`(n)/(3) \geq -4` and
`(n)/(-5)\geq 1`, let's solve the inequality separately.

Given that:

`(n)/(3) \geq -4`

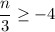
Let's multiply both sides by 3

`(n)/(3) * 3 \geq -4 * 3`

`n \geq -12`

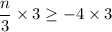
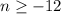
Similarly,
`(n)/(-5)\geq 1`

Multiply both sides by -5

`(n)/(-5) * -5 \geq 1 * -5`

`n \leq -5`

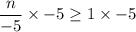
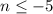
We can write the solution set of the compound inequality as:

-12 ≤ n ≤ -5. It implies that n is greater than or equal to -12 and less than or equal to -5. The graph of the inequality is shown below.