Question

State a, b, and the y-intercept then graph the function and describe the end behavior of the grpahs

Answer 1

9514 1404 393

Answer:

9. a = 3, b = 3, y-intercept = 3

10. a = 5, b = 0.6, y-intercept = 5

Explanation:

The picture is fuzzy, but we think the given equations are ...

`\text{9. }f(x)=3(3)^x\\ \text{10. }f(x)=5(0.6)^x`

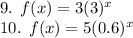
You are comparing these to the form ...

`f(x) = a(b)^x`

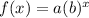
so the values of 'a' and 'b' should be readily identifiable. The y-intercept in each case is y = a.

The end behavior depends on whether b > 1 or not. Growth functions (b>1) go to 0 on the left and ∞ on the right. Decay functions (b<1) are the reverse.

__

9. a = 3, b = 3, y-intercept = 3

The end behaviors are (x, f(x)) ⇒ (-∞, 0), (∞, ∞).

__

10. a = 5, b = 0.6, y-intercept = 5

The end behaviors are (x, f(x)) ⇒ (-∞, ∞), (∞, 0).