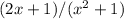Question

Algebra 2
Adding subtracting rational expressions with denominators

Answer 1

The sum of the given fractions is
`(2x + 1)/(x^2+1)`

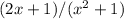
To find the sum of the fractions
`(x-2)/(x^2+1)` and
`(x+3)/(x^2+1)` , we can follow these steps:

Step 1: Identify the common denominator:

Both fractions have the same denominator, which is
`x^2 + 1.`

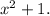
Step 2: Rewrite the fractions with the common denominator:

`(x-2)/(x^2+1) + (x+3)/(x^2+1)`

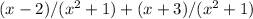
Step 3: Combine the numerators:

(x-2) + (x+3)

Step 4: Simplify the numerator:

x - 2 + x + 3

Step 5: Combine like terms:

2x + 1

Step 6: Write the final sum:

The sum of the fractions
`(x-2)/(x^2+1) + (x+3)/(x^2+1) is (2x + 1)/(x^2+1)`.

In conclusion, the sum of the given fractions is
`(2x + 1)/(x^2+1)`.

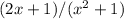Therefore the correct answer is
`(2x + 1)/(x^2+1)`