Question

Fifty seven percent of employees judge their peers by the cleanliness of their workspaces. You randomly select 10 employees and ask them whether they judge their peers by the cleanliness of their workspaces. The random variable represents the number of employees who judge their peers by the cleanliness of their workspaces

Answer 1

a) The table is as below.

b) The values that can be considered unusual are 0.094718, 0.082258 , 0.083484 and 0.000071 .

How to construct binomial probability

The binomial probability formula:

`P(x = k) = ⁿCk {p}^(k) {( -1 - p)}^(n - k)`

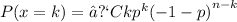
Where:

n is the number of trials (10 employees)

k is the number of successes (employees judging their peers),

p is the probability of success (57% or 0.57).

x = 0, 1, 2, ..., 10.

P(X = 0) = 1 *0.57⁰ * (1 - 0.57)¹⁰ = 0.000071

P(X = 1) = 10 *0.57¹* (1 - 0.57)⁹ = 0.000945

P(X = 2) = 45 *0.57²*(1 - 0.57)⁸ = 0.006269

P(X = 3) = 120 *0.57³ *(1 - 0.57)⁷= 0.022048

P(X = 4) = 210 *0.57⁴ *(1 - 0.57)⁶ = 0.051212

P(X = 5) = 252*0.57⁵*(1 - 0.57)⁵ = 0.082258

P(X = 6) = 210 *0.57⁶*(1 - 0.57)⁴ = 0.094718

P(X = 7) = 120 *0.57⁷ * (1 - 0.57)³ = 0.083484

P(X = 8) = 45 *0.57⁸*(1 - 0.57)² = 0.055186

P(X = 9) = 10 *0.57⁹*(1 - 0.57)¹ = 0.024377

P(X = 10) = 1 *0.57¹⁰*(1 - 0.57)⁰ = 0.005131

b) The values that can be considered unusual are

0.094718, 0.082258 , 0.083484 and 0.000071 .

They are too high and low considering critical value of 0.024377.

Complete question