Question

Find the real solution(s) of the following equation. s^3 = 729

a. s=7
b. s=-7
c. s=9
d. s=-9
e. none

Answer 1

Hi there! I'd be happy to help you with that equation. To find the real solutions of the equation s^3 = 729, we need to find the value of s that, when raised to the power of 3, equals 729.

To solve this, we can take the cube root of both sides of the equation. The cube root of 729 is 9, since 9 * 9 * 9 equals 729.

So, the real solution to the equation s^3 = 729 is s = 9.

Therefore, the correct answer is c. s=9.

Great job! Is there anything else you'd like to learn about this topic, or do you have any other questions?

Answer 2

Answer: C, s=9

Explanation:

How your teacher wants it:

We start off with our equation:
`s^3=729`

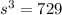
From there we need to isolate s. Remember, to get rid of an exponent you can multiply it by its reciprocal. In this case we take 3 --> 1/3. And, we multiply it by both sides.

So we get
`s=729^(1/3)`

From there we take the root property and make
`s=\sqrt[3]{729}`

Plug it in your calculator and get s=9

How you can do it fast:

Just remember this rule: root the other side with the exponent

In this case the exponent is 3, so take
`\sqrt[3]{729}` on the right side.