Question

There is a parallel plate capacitor. Both plates are 4x2 cm and are 10 cm apart. The top plate has surface charge density of 10C/m^2 and the bottom plate has a surface charge density of -10C/m^2. Find the total charge on each plate. Find the electric field at the point exactly midway between the plates. Find the electric potential between the two plates. If an electron was in the middle the two plates, find the force on it.

Answer 1

1) The total charge of the top plate is 0.008 C

b) The total charge of the bottom plate is -0.008 C

2) The electric field at the point exactly midway between the plates is 0

3) The electric field between plates is approximately 1.1294 × 10¹² N/C

4) The force on an electron in the middle of the two plates is approximately 1.807 × 10⁻⁷ N

Step-by-step explanation:

The given parameters of the parallel plate capacitor are;

The dimensions of the plates = 4 × 2 cm

The distance between the plates = 10 cm

The surface charge density of the top plate, σ₁ = 10 C/m²

The surface charge density of the bottom plate, σ₂ = -10 C/m²

The surface area, A = 0.04 m × 0.02 m = 0.0008 m²

1) The total charge of the top plate, Q = σ₁ × A = 0.0008 m² × 10 C/m² = 0.008 C

b) The total charge of the bottom plate, Q = σ₂ × A = 0.0008 m² × -10 C/m² = -0.008 C

2) The electrical field at the point exactly midway between the plates is given as follows;

`V_(tot) = V_(q1) + V_(q2)`

`V_q = (k \cdot q)/(r)`

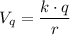
Therefore, we have;

The distance to the midpoint between the two plates = 10 cm/2 = 5 cm = 0.05 m

`V_(tot) = (k \cdot q)/(0.05) + (k \cdot (-q))/(0.05) = (k \cdot q)/(0.05) - (k \cdot q)/(0.05) = 0`

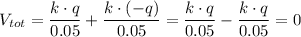
The electric field at the point exactly midway between the plates,
`V_(tot)` = 0

3) The electric field, 'E', between plates is given as follows;

`E =(\sigma )/(\epsilon_0 ) = (10 \ C/m^2)/(8.854 * 10^(-12) \ C^2/(N\cdot m^2)) \approx 1.1294 * 10^(12)\ N/C`

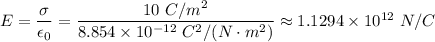
E ≈ 1.1294 × 10¹² N/C

The electric field between plates, E ≈ 1.1294 × 10¹² N/C

4) The force on an electron in the middle of the two plates

The charge on an electron, e = -1.6 × 10⁻¹⁹ C

The force on an electron in the middle of the two plates,
`F_e` = E × e

∴
`F_e` = 1.1294 × 10¹² N/C × -1.6 × 10⁻¹⁹ C ≈ 1.807 × 10⁻⁷ N

The force on an electron in the middle of the two plates,
`F_e` ≈ 1.807 × 10⁻⁷ N