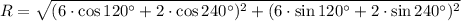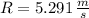Question

Find the sum of each pair of vectors and match it with the magnitude of the resultant vector.

Answer 1

By definitions of vectors and magnitude of vectors, the magnitudes of the sum of two vectors are, respectively: Case 1:
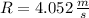`R = 4.052\,(m)/(s)`, Case 2:
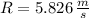`R = 5.826\,(m)/(s)`, Case 3:
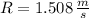`R = 1.508\,(m)/(s)`, Case 4:
`R = 5.291\,(m)/(s)`

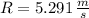
How to determine the magnitude of the sum of two vectors

In this problem we must determine the magnitude of the sum of each pair of vectors. Vectors are expressions of the form:

`\vec v = r\cdot (\cos \theta\,\hat{i} + \sin \theta\,\hat{j})`

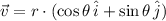
Where:

• r - Magnitude
• θ - Direction, in degrees.

And the magnitude of the sum of the pair of vectors is done by Pythagorean theorem:

`R = \sqrt{(r_(1)\cdot \cos \theta_(1)+r_(2)\cdot \cos \theta_(2))^2+(r_(1)\cdot \sin \theta_(1)+r_(2)\cdot \sin \theta_(2))}`

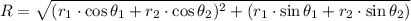
Now we proceed to determine the magnitude for each case:

Case 1:

`R = √((3.5\cdot \cos 35^\circ + 4\cdot \cos 150^\circ)^2+(3.5 \cdot \sin 35^\circ + 4 \cdot \sin 150^\circ)^2)`

`R = 4.052\,(m)/(s)`

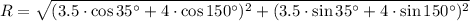
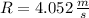
Case 2:

`R = \sqrt{(4.5\cdot \cos 55^\circ + 3\cdot \cos 135^\circ)^2 + (4.5\cdot \sin 55^(\circ)+3\cdot \sin 135^\circ)^2}`

`R = 5.826\,(m)/(s)`

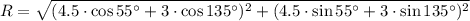
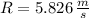
Case 3:

`R = √((3\cdot \cos 70^\circ + 5\cdot \cos 210^\circ)^2+(3\cdot \sin 70^\circ + 5\cdot \sin 210^\circ)^2)`

`R = 1.508\,(m)/(s)`

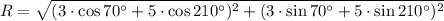
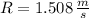
Case 4:

`R = √((6\cdot \cos 120^\circ + 2\cdot \cos 240^\circ)^2+(6\cdot \sin 120^\circ + 2\cdot \sin 240^\circ)^2)`

`R = 5.291\,(m)/(s)`