At the 0.05 level of significance, there is not enough evidence to conclude that the population mean height of treated begonias is different from the reported mean of 33 centimeters.
To determine whether the population mean height of treated begonias (μ) is different from the reported mean (33 centimeters), you can perform a two-tailed t-test. The null hypothesis (H_0 ) is that the population mean is equal to the reported mean, and the alternative hypothesis (H_a) is that the population mean is different from the reported mean.
The hypotheses are:
H_0=33/H_0
H_a :μ/33
The test statistic for a two-tailed t-test is calculated using the formula:
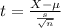
where:
X is the sample mean,
μ is the population mean under the null hypothesis,
s is the sample standard deviation,
n is the sample size.
Given:
X =30 centimeters
μ_0 =33 centimeters (the population mean under the null hypothesis)
s=7 centimeters
n=12 (sample size)
Let's calculate the test statistic:
t=
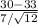
t≈−1.481
Now, we need to compare this test statistic to the critical value at a 0.05 level of significance with df=n−1=11 degrees of freedom.
You can use a t-distribution table or a statistical software to find the critical values. For a two-tailed test at a 0.05 significance level with 11 degrees of freedom, the critical values are approximately
±2.201.
Since −1.481 is within the range −2.201 to 2.201, we fail to reject the null hypothesis.
Conclusion: At the 0.05 level of significance, there is not enough evidence to conclude that the population mean height of treated begonias is different from the reported mean of 33 centimeters.