Question

2) If y = 7 is a horizontal asymptote of a rational function f, then which of the following must be true

2)
(a)
lim
fX）=8
x→7
li
f(x) = 7
(c).
lim
×→0
f(x) = 7
= 0
f(x) = -7

Answer 1

When y equals 7, Since it's a horizontal asymptote of a rational function f(x), the values of f(x) tend to approach 7 as x approaches positive or negative infinity.

Considering the options:

`(a) \(\lim_(x \to 7) f(x) = 8\)`

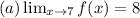
The fact that y = 7 is a horizontal asymptote does not inevitably imply this conclusion. The asymptote does not define the limit when x approaches 7 from either side.

(b) f(x) equals 7.

This claim may not always be accurate. The function does not always equal the asymptote when it has a horizontal asymptote.

`(c), \(\lim_(x \to 0) f(x) = 7\)`

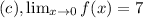
This assertion is not inherently supported by the fact that y = 7 is a horizontal asymptote. The asymptote at x = 7 is not directly related to the limit as x approaches 0.

Because y = 7 is a horizontal asymptote, none of the options must be true. The right answer is that f(x) approaches 7 as x approaches either positive or negative infinity.