Question

Which of the following is the graph of (x – 2)2 + (y – 1)2 = 12.25?

a. circle with center at 2 comma negative 1 and circle passes through the point 5 and 5 tenths comma negative 1
b. circle with center at negative 2 comma 1 and circle passes through the point 1 and 5 tenths comma 1
c. circle with center at 2 comma 1 and circle passes through the point 5 and 5 tenths comma 1
d. circle with center at negative 2 comma negative 1 and circle goes through the point 1 and 5 tenths comma negative 1

Answer 1

C) Circle with center at (2, 1) and circle passes through the point (5.5, 1).

Explanation:

The general equation of a circle is:

`(x - h)^2 + (y-k)^2 = r^2`

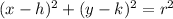
where:

• (h, k) is the center.
• r is the radius.

Comparing the given equation, (x - 2)² + (y - 1)² = 12.25, with the general equation of a circle:

• Center = (2, 1)
• r² = 12.25

The radius can be calculated as follows:

`\begin{aligned}r^2&=12.25\\√(r^2)&=√(12.25)\\r&=3.5\end{aligned}`

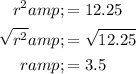
So, the graph of the circle represented by the equation (x - 2)² + (y - 1)² = 12.25 has:

• Center = (2, 1)
• Radius = 3.5

To determine if the circle passes through point (5.5, 1), we can substitute x = 5.5 and y = 1 into the equation:

`\begin{aligned}(5.5-2)^2+(1-1)^2&\overset{?}=12.25\\\\(3.5)^2+(0)^2&\overset{?}=12.25\\\\12.25&\overset{\checkmark}=12.25\end{aligned}`

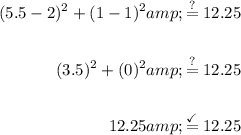
Therefore, this confirms that the circle passes through point (5.5, 1). So the description of the graph of the given equation is option C.