Question

A ferris wheel has a diameter of 16 m, with a minimum height of 2 m above the ground. It takes 20 seconds for the ferris wheel to complete one rotation. If a rider boards a car when it is at its lowest point: a) Determine an equation to model the rider’s height after t seconds. b) Sketch a graph of two full revolutions for the rider. c) Determine the height of the rider after 8 seconds. d) Determine the first two times the rider reaches a height of 12 metres.

Answer 1

a) An equation to model the rider’s height after t seconds is
`\(h(t) = 8\sin\left((\pi)/(10)t\right) + 10\)`.
b) Above sketch a sinusoidal wave starting at 18m, dipping to 2m.
c) The height of the rider after 8 seconds is
`\(h(8) \approx 16\, \text{m}\)`.
d) The first two times the rider reaches a height of 12 metres is 9.55 and 30.45

a) The equation to model the rider's height is
`\(h(t) = 8\sin\left((\pi)/(10)t\right) + 10\).`

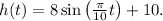
b) Sketch a graph of two full revolutions with a sinusoidal wave starting at a maximum height of 18 m, descending to a minimum of 2 m, rising to a maximum of 18 m again, and completing the cycle.

c) To find the height after 8 seconds, substitute t = 8 into the equation:

`\(h(8) = 8\sin\left((\pi)/(10) * 8\right) + 10 \approx 16\, \text{m}\).`

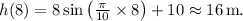
d) To find the first two times the rider reaches a height of 12 m, solve the equation
`\(8\sin\left((\pi)/(10)t\right) + 10 = 12\)`.

The solutions are
`\(t \approx 9.55\)` seconds and

`\(t \approx 30.45\)` seconds.