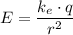Question

A point charge q is located at the center of a spherical shell of radius a that has a charge −q uniformly distributed on its surface. Find the electric field for the following points: (a) for all points outside the spherical shell E = keq2/r2 E = q/4πr2 none of these E = keq/r2 E = 0 (b) for a point inside the shell a distance r from the center E = keq2/r2 E = keq/r2 E = 0 E = q/4πr2 none of these

Answer 1

a) E = 0

b)
`E = (k_e \cdot q)/( r^2 )`

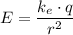
Step-by-step explanation:

The electric field for all points outside the spherical shell is given as follows;

a)
`\phi_E = \oint E \cdot dA = (\Sigma q_(enclosed))/(\varepsilon _(0))`

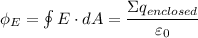
From which we have;

`E \cdot A = \frac{{\Sigma Q}}{\varepsilon _(0)} = (+q + (-q))/(\varepsilon _(0)) = (0)/(\varepsilon _(0)) = 0`

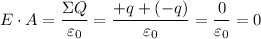
E = 0/A = 0

E = 0

b)
`\phi_E = \oint E \cdot dA = (\Sigma q_(enclosed))/(\varepsilon _(0))`

`E \cdot A = (+q )/(\varepsilon _(0))`

`E = (+q )/(\varepsilon _(0) \cdot A) = (+q )/(\varepsilon _(0) \cdot 4 \cdot \pi \cdot r^2)`

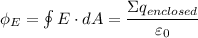
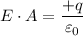
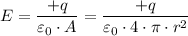
By Gauss theorem, we have;

`E\oint dS = (q)/(\varepsilon _(0))`

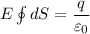
Therefore, we get;

`E \cdot (4 \cdot \pi \cdot r^2) = (q)/(\varepsilon _(0))`

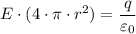
The electrical field outside the spherical shell

`E = (q)/(\varepsilon _(0) \cdot (4 \cdot \pi \cdot r^2) )= (q)/(4 \cdot \pi \cdot \varepsilon _(0) \cdot r^2 )= (q)/((4 \cdot \pi \cdot \varepsilon _(0) )\cdot r^2 )`

`k_e= (1)/((4 \cdot \pi \cdot \varepsilon _(0) ) )`

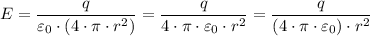
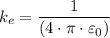
Therefore, we have;

`E = (k_e \cdot q)/( r^2 )`