Question

Could you provide qualities of a Cardioid Limacon?

Answer 1

A cardioid limaçon is a polar graph that exhibits the following qualities: It is a type of limaçon, a shape obtained by tracing a point on the circumference of a circle as it rolls around the outside of another fixed circle. The cardioid limaçon is characterized by a single loop with a cusp, resembling a heart shape. Its equation in polar coordinates is typically given by \(r = a + b\cos\theta\), where \(a\) and \(b\) are constants determining the size and shape of the limaçon.

Step-by-step explanation:

A cardioid limaçon is a specific type of limaçon, a family of curves generated by the motion of a point on the circumference of one circle as it rolls around the outside of another fixed circle. In the case of a cardioid limaçon, its defining feature is the shape of a heart, resembling the outline of a valentine. The equation
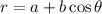`\(r = a + b\cos\theta\)` describes this curve in polar coordinates, where a and b\ are constants determining the size and shape of the limaçon.

The constant a represents the distance from the pole to the cusp of the heart, and b determines the size of the loop. The parameter
`\(\theta\)` represents the angle measured in radians. When
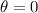`\(\theta = 0\)`, the polar equation evaluates to r = a + b, giving the distance from the pole to the outer loop of the cardioid limaçon.

Understanding the qualities of a cardioid limaçon involves recognizing its unique geometric properties and interpreting the parameters in its polar equation. This mathematical concept is often encountered in polar coordinate systems and provides a visually appealing representation of a heart-shaped curve.