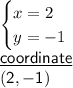Question

Solve the system of linear equations below: y= 4x-9 y= x-3​

Answer 1

(2, - 1 )

Explanation:

Given the 2 equations

y = 4x - 9 → (1)

y = x - 3 → (2)

Substitute y = 4x - 9 into (2)

4x - 9 = x - 3 ( subtract x from both sides )

3x - 9 = - 3 ( add 9 to both sides )

3x = 6 ( divide both sides by 3 )

x = 2

Substitute x = 2 into either of the 2 equations for corresponding value of y

Substituting into (2)

y = 2 - 3 = - 1

solution is (2, - 1 )

Answer 2

Explanation

• Given the system of equations.

`\begin{cases} y = 4x - 9 \\ y = x - 3 \end{cases}`

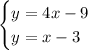
We can combine both equations

`4x - 9 = x - 3`

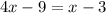
Solve the equation.

`4x - x = 9 - 3 \\ 3x = 6 \\ x = (6)/(3) \longrightarrow (2)/(1) \\ x = 2`

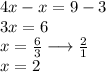
Then we substitute the value of x in any given equations which I will be substituting in the second equation

`y = x - 3 \\ y = 2 - 3 \\ y = - 1`

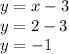
Therefore, from x = 2 and y = -1, the solution is (2,-1)

Answer Check

Substitute the value of x and y in both equations.

First Equatio

`y = 4x - 9 \\ - 1 = 4(2) - 9 \\ - 1 = 8 - 9 \\ - 1 = - 1`

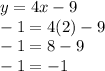
Second Equation

`y = x - 3 \\ - 1 = 2 - 3 \\ - 1 = - 1`

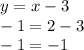
Both equations are true for (2,-1).

Answer

`\begin{cases} x = 2 \\ y = - 1 \end{cases} \\ \sf \underline{coordinate} \\ (2,-1)`