Question

The equation of a line containing one leg of a right triangle is y=-4x. Which of the following equations could represent the line containing the other leg of this triangle?

Answer 1

The correct equation representing the line containing the perpendicular leg is
`\(y = (1)/(4)x + 2\).`

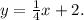
To find the equation of the line containing the perpendicular leg of the right triangle, we need to determine the negative reciprocal of the slope of the given line. The equation of the given line is y = -4x, and its slope is -4.

The negative reciprocal of -4 is 1/4, so the slope of the perpendicular line is 1/4. Now, we need to check which of the given equations has a slope of 1/4 and passes through the same point as the original line.

1.
`\(y = (1)/(4)x + 2\)` - This equation has a slope of 1/4, so it represents the line containing the perpendicular leg.

2. y = 4x - This equation has a slope of 4, not 1/4.

3. y = -4x + 2 - This equation has the same slope as the original line, not the negative reciprocal.

4.
`\(y = -(1)/(4)x\)` - This equation has the negative reciprocal slope but does not pass through the same point.

Therefore, the correct equation representing the line containing the perpendicular leg is
`\(y = (1)/(4)x + 2\).`

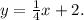
The probable question may be:

The equation of a line containing one leg of a right triangle is y=-4x. Which of the following equations could represent the line containing the perpendicular leg of this right triangle?

1. y = 1/4x +2

2. y = 4x

3. y= -4x+2

4. y = -1/4x