Question

9 i don't know how to do

Answer 1

9. see below for proof; θ ∈ {45°, 135°, 225°, 315°}

11. see below for proof; x ∈ {109.47°, 250.53°}

Explanation:

You want to prove two trig identities, then use those to solve trig equations.

9. 2tan²(θ)sin²(θ) = 1

It is often useful to use the identities ...

• tan = sin/cos
• sin² +cos² = 1

(i) Doing that here, we get ...

`2\tan^2\theta \sin^2 \theta=1\\\\2(\sin^2\theta)/(\cos^2\theta)\sin^2\theta=1\qquad\text{replace tan}\\\\(2\sin^4\theta)/(1-\sin^2\theta)=1\qquad\text{replace $\cos^2$}\\\\2\sin^4\theta=1-\sin^2\theta\qquad\text{multiply by $(1-\sin^2\theta)$}\\\\2\sin^4\theta+\sin^2\theta-1=0\qquad\text{put in standard form}`

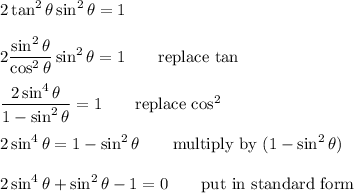
(ii) Substituting x=sin²(θ), we have the quadratic ...

2x² +x -1 = 0

The quadratic formula gives the solutions as ...

x = (-1 ±√(1 -4(2)(-1)))/(2(2)) = (-1±3)/4 = -1, 1/2

The value of sin(θ) is the square root of these values. √-1 is imaginary, so does not give us any solutions. √(1/2) = (±√2)/2, corresponding to ...

sin(θ) = (±√2)/2

θ ∈ {45°, 135°, 225°, 315°}

11. sin(x)tan(x)/(1 -cos(x)) = 1 + 1/cos(x)

(i) Substituting as suggested above, we have ...

`(\sin x\tan x)/(1-\cos x)=1+(1)/(\cos x)\\\\(\sin^2 x)/(\cos x(1-\cos x))=\qquad\text{substitute for $\tan x$}\\\\(1-\cos^2 x)/(\cos x(1-\cos x))=\qquad\text{substitute for $\sin^2 x$}\\\\(1+\cos x)/(\cos x)=1+(1)/(\cos x)\qquad\text{cancel the common factor}\\\\1+(1)/(\cos x)=1+(1)/(\cos x)\qquad\text{Q.E.D.}`

(ii) Using this result, the equation can be written ...

(1 +1/cos(x)) +2 = 0

1/cos(x) = -3 . . . . . . . . . subtract 3

x = arccos(-1/3) . . . . . . . solve for x

x ∈ {109.47°, 250.53°} . . . . approximately