Answer:
Part A: The lengths of the sides are
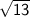 ,
,
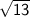 , and
, and
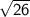 .
.
Part B: The slopes of the sides are
 ,
,
 , and
, and
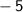 .
.
Part C: The triangle is classified as right angled isoceles triangle.
Explanation:
Let's work through each part of the problem:
Part A:
The distance between two points
 and
and
 in a Cartesian plane is given by the distance formula:
in a Cartesian plane is given by the distance formula:

Side AB:
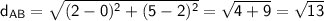
Side BC:

Side CA:


Part B:
The slope (
 ) between two points
) between two points
 and
and
 is given by:
is given by:

Slope of AB:

Slope of BC:
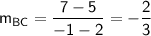
Slope of CA:
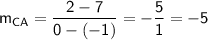

Part C:
To determine if the triangle, we need to check if any of the angles are right angles (90 degrees) and if any two or three sides have the same length.
From Part A, we found that the lengths of the sides are:
Now, let's check the slopes from Part B:
The negative reciprocal of the slope of
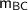 (
(
 ) is
) is
 (5), which indicates that the angle between sides BC and CA is a right angle.
(5), which indicates that the angle between sides BC and CA is a right angle.
Additionally, sides AB and BC have the same length (
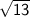 ).
).
Therefore, the triangle is a right-angled isosceles triangle.