Question

The rational function g is given by 9(2) = -1000 = (2+10)(2 -10x+10

Which of the following statements describes the behavior of the graph of g?

Answer 1

A statement that best describes the behavior of the graph of g is: b. The graph has a hole at x = −10 because (x + 10) appears exactly once, when both the numerator and the denominator of g are factored.

In Mathematics and Euclidean Geometry, a hole is a point on the graph of a rational function where the input value causes both its numerator and denominator to be equal to zero (0).

By factorizing the numerator and denominator of the given rational function, we have the following:

`g(x)=(x^3+1000)/(x^2-100) \\\\g(x)=((x+10)(x^2-10x+1000))/((x+10)(x-10))\\\\g(x)=((x^2-10x+1000))/((x-10))`

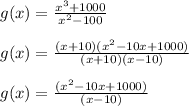
In this context, we can logically deduce that the graph of the given rational function has a hole at x = -10 because (x + 10) appears exactly once, when both the numerator and the denominator of g are factored;

Holes = (-10, -15).

In conclusion, we can logically deduce that this rational function neither has an x-intercept, a vertical asymptote nor a horizontal asymptote.

Complete Question:

The rational function g is given by
`g(x)=(x^3+1000)/(x^2-100) =((x+10)(x^2-10x+1000))/(x^2-100)`. Which of the following statements describes the behavior of the graph of g?

a. The graph intersects the x-axis at x=−10 because
`(-10)^3+1000=0`.

b. The graph has a hole at x=−10 because (x+10) appears exactly once, when both the numerator and the denominator of g are factored

c.The graph has vertical asymptotes at x=10 and at x=−10 because
`10^2 -100=0` and
`(-10)^2-100=0`.

d.The graph has no holes because the degree of the numerator is greater than the degree of the denominator.