Question

Given f(x) = x² - 9, find the indicated values:

Answer 1

Given
`\(f(x) = x^2 - 9\`, to find the indicated values, we'll solve for specific inputs:

a) f(3)

b) f(-4)

Step-by-step explanation:

a) To find f(3), substitute x = 3 into the function f(x).

`\(f(3) = (3)^2 - 9 = 9 - 9 = 0\).`

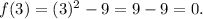
Hence, f(3) = 0).

b) For f(-4), substitute x = -4 into the function f(x).

`\(f(-4) = (-4)^2 - 9 = 16 - 9 = 7\).`

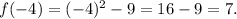
Therefore, f(-4) = 7.

Explanation:

To determine f(3), we substitute x = 3 into the function
`\(f(x) = x^2 - 9\)`. By direct substitution,
`\(f(3) = (3)^2 - 9\)`, which simplifies to 9 - 9 = 0. Therefore, f(3) = 0. This signifies that when the input is 3, the output of the function is 0.

Next, evaluating
`\(f(-4)\)` involves substituting
`\(x = -4\)` into the function. By direct substitution,
`\(f(-4) = (-4)^2 - 9\)`, which simplifies to
`\(16 - 9 = 7\)`. Consequently,
`\(f(-4) = 7\)`. This indicates that when the input is -4, the output of the function is 7.

In summary,
`\(f(3) = 0\)` and
`\(f(-4) = 7\)` are the respective values obtained when the function
`\(f(x) = x^2 - 9\)` is evaluated at inputs 3 and -4, demonstrating the output corresponding to each specific input value.