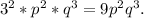Final answer:
The greatest common factor of the given expressions is
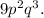
Step-by-step explanation:
To find the greatest common factor of
 ^4, and
^4, and
 ed to determine the highest power of each variable that appears in all three expressions. Let's break down each expression:
ed to determine the highest power of each variable that appears in all three expressions. Let's break down each expression:
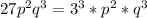
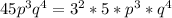
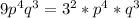
We can see that the highest power of 3 that appears in all three expressions is
 imilarly, the highest power of p is
imilarly, the highest power of p is
 d the highest power of q is
d the highest power of q is
 herefore, the greatest common factor is
herefore, the greatest common factor is