Question

A Van de Graaff generator is one of the original particle accelerators and can be used to accelerate charged particles like protons or electrons. You may have seen it used to make human hair stand on end or produce large sparks. One application of the Van de Graaff generator is to create x-rays by bombarding a hard metal target with the beam. Consider a beam of protons at 1.10 keV and a current of 4.65 mA produced by the generator.

(a) What is the speed of the protons?
(b) How many protons are produced each second?

Answer 1

Given that :

The energy of the protons, K.E. = 1.10 keV

`$= 1.10 * 10^3 \ eV $`

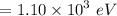
The current produced by the generator is I = 5 mA

`$= 5 * 10^(-3) \ A$`

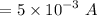
Now
`$1 \ eV = 1.6 * 10^(-19 )\ J$`

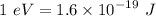
Mass of the proton, m =
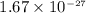`$1.67 * 10^_(-27) $` kg

Charge of the proton,
`$q_p = 1.6 * 10^(-19) \ C$`

a). Therefore using the formula for K.E. we can find out the velocity of the proton.

`$K.E. =(1)/(2)mv^2$`

`$v=\sqrt{(2K.E.)/(m)}$`

`$v=\sqrt{(2* 10^3 * 1.6 * 10^(-19))/(1.67 * 10^(-27))}$`

`$= 4.38 * 10^5 \ m/s$`

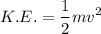
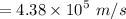
b). We know that the current is :

`$I=(\Delta Q)/(\Delta t)$`

Therefore, the total charge in one second is given by :

`$\Delta Q = I * \Delta t$`

`$= 5 * 10^(-3) * 1$`

`$= 5 * 10^(-3)\ C$`

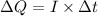
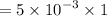
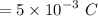
So, the number of protons in this charge is given by :

`$n = (\Delta Q)/(q_p)$`

`$=(5 * 10^(-3) )/(1.6 * 10^(-19))$`

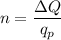
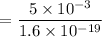
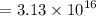`$= 3.13 * 10^(16)$` protons