Question

Your department has found that the concentration of the new drug in a patient's bloodstream can be modeled by the equation C(t)=__5t t²+1 where C(t) represents the milligrams per liter of the drug and t represents the number of hours after the drug is administered. Graph the asymptote, and identify and interpret the horizontal asymptote of the function..

Answer 1

The horizontal asymptote y=5 represents the long-term behavior of the drug concentration in the patient's bloodstream.

The given equation for the concentration of the drug in a patient's bloodstream is:

`C(t)= (5t)/(t^2+1)`

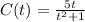
​To identify the horizontal asymptote, we'll look at the behavior of the function as t approaches positive or negative infinity.

For a rational function like this one, the degree of the numerator is the same as the degree of the denominator. In this case, both the numerator and denominator have a degree of 2. When the degrees are the same, the horizontal asymptote can be found by dividing the coefficient of the term with the highest degree in the numerator by the coefficient of the term with the highest degree in the denominator.

In this case, the coefficient of the t^2 term in the numerator is 5, and the coefficient of the t^2 term in the denominator is 1.

So, the horizontal asymptote is at y= 5/1 =5.

Let's graph the function and see the behavior as t approaches positive or negative infinity. However, keep in mind that I can't draw graphs directly here, but I'll describe how the graph looks:

As t approaches positive infinity, the function approaches the horizontal line

y=5.

As t approaches negative infinity, the function also approaches the horizontal line y=5.

There will be a vertical asymptote at t=0 since the denominator becomes 0 when t=0.

So, the horizontal asymptote y=5 represents the long-term behavior of the drug concentration in the patient's bloodstream. It means that as time goes on (approaching infinity), the concentration will approach a maximum value of 5 milligrams per liter.