Solution :
Assuming that the wire has an uniform temperature, the equivalent convective heat transfer coefficient is given as :
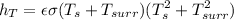
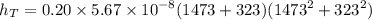
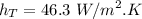
The total heat transfer coefficient will be :
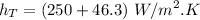

Now calculating the maximum volumetric heat generation :
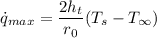
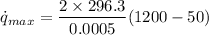
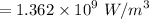
The heat generation inside the wire is given as :
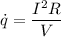
Here, R is the resistance of the wire
V is the volume of the wire
∴
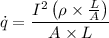
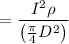
where, ρ is the resistivity.
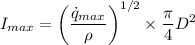
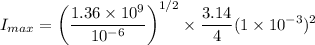
= 28.96 A
Now considering the relation for the current flow through the finite potential difference.
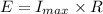
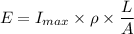

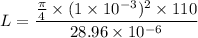
= 2.983 m
Now calculating the power rating of the heater:
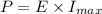
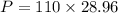
= 3185.6 W
= 3.1856 kW