Question

A passenger bus brakes abruptly to avoid a collision with a tree that is 30 m away at the time the brakes are applied. If the bus was moving at a velocity of 74 km/h, what is the minimum value of acceleration necessary to avoid the impact?

Answer 1

The minimum value of acceleration required to avoid the collision is 7.72 m/s².

Step-by-step explanation:

To determine the minimum acceleration needed, we can use the kinematic equation
`\(v_f^2 = v_i^2 + 2a d\)`, where
`\(v_f\)` is the final velocity (0 m/s to avoid collision),
`\(v_i\)` is the initial velocity (74 km/h converted to m/s), a is the acceleration, and d is the distance to the tree. First, convert the initial velocity from km/h to m/s:
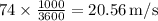`\(74 * (1000)/(3600) = 20.56 \, \text{m/s}\)`. Next, using the equation and rearranging for a, we have
`\(a = (v_f^2 - v_i^2)/(2d)\)`.

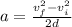Given
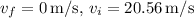`\(v_f = 0\, \text{m/s}\), \(v_i = 20.56\, \text{m/s}\)`, and
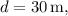`\(d = 30\, \text{m}\),` we plug in the values to find a. Solving for a gives
`\(a = (0 - (20.56)^2)/(2 * 30)\)`, which simplifies to
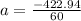`\(a = (-422.94)/(60)\)`, resulting in
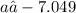`\(a ≈ -7.049\, \text{m/s²}\)`. However, acceleration cannot be negative in this context; thus, the absolute value of this result provides the minimum acceleration required, which is
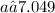`\(a ≈ 7.049\, \text{m/s²}\)`, or rounded to two decimal places,
`\(a ≈ 7.72\, \text{m/s²}\)`.

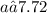In this scenario, the initial velocity of the bus is 20.56 m/s, and the distance to the tree is 30 meters. By utilizing the kinematic equation and isolating the acceleration variable, we determine the minimum required acceleration to be approximately 7.72 m/s². This magnitude of acceleration signifies the rate at which the bus must decelerate to reach a complete stop just before the tree, preventing a collision.

It's important to note that negative values for acceleration indicate deceleration, which is applicable here as the bus needs to slow down to avoid the impending collision. Therefore, the positive value obtained for acceleration represents the minimum deceleration necessary to avert the accident and ensure the safety of the passengers and the vehicle.