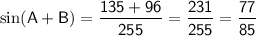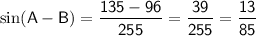Answer:
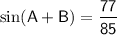
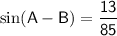
Explanation:
To find
 and
and
 , we can use the sum and difference formulas for sine:
, we can use the sum and difference formulas for sine:
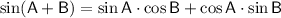
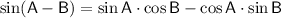
Given that
 and
and
 , we need to find
, we need to find
 and
and
 .
.
First, let's find
 using the fact that
using the fact that
 :
:
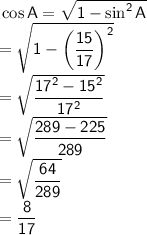
Now, let's find
 using the fact that
using the fact that
 :
:

Now, we can substitute these values into the sum and difference formulas:
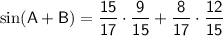
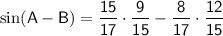
Let's simplify these expressions: