Question

palindrome is a string whose reversal is identical to the string. how many bit strings of length n are palindromes if n is even and if n is odd? (you must provide an answer before moving to the next part.)

Answer 1

Number of odd-length palindromes =
`2^n + 2^(n-1)`

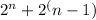
1. A length-n even palindrome can be viewed as two halves, mirrored across the center. Each half has n/2 bits.

2. For each half, any combination of the two possible values (0 or 1) is valid.

3. Therefore, the number of possibilities for each half is
`2^(n/2).`

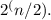
4. Since both halves are independent, the total number of palindromes is obtained by multiplying the possibilities for each half:
`2^(n/2) * 2^(n/2)` =
`2^(n/2 + n/2) = 2^n.`

1. An odd-length palindrome has (n-1)/2 bits on each side of the center bit.

2. Similar to even lengths, each side can be any combination of 0 or 1, totaling 2^((n-1)/2) possibilities each.

3. However, unlike even lengths, the center bit also counts. It contributes another 2 possibilities (0 or 1).

4. Therefore, the final number of palindromes considers both side possibilities and the center bit:
`2^((n-1)/2) * 2^((n-1)/2) * 2 = 2^((n-1)/2 + (n-1)/2 + 1) = 2^(n-1) * 2 = 2^n + 2^(n-1).`