Question

Solve the differential equation below, subject to the given initial condition. Assume t > 0 .

dx/dt= x ln x/t , x(1) = 3
x(t) =

Answer 1

The solution to the given differential equation dx/dt = xln(x)/t with the initial condition x(1)=3 is x(t)=3tln(t).

To solve the differential equation, we can separate variables and integrate both sides. Starting with the given equation:

`(dx)/(dt) = (xln(x))/(t)`

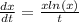
Separating variables:

`(1)/(x) (dx)/(ln(x)) = (1)/(t) dt`

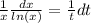
Integrating both sides:​

∫
`(1)/(t)`
`\int\ {(1)/(x) } \, dx = \int\ {(1)/(t) } \, dt`

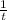
This leads to:

ln(∣ln(x)∣)=ln(∣t∣)+C₁

Solving for ∣ln(x)∣:

∣ln(x)∣=e^(ln(∣t∣)+C₁)

Simplifying, we get:

∣ln(x)∣=C₂∣t∣

Now, consider the initial condition x(1)=3:

∣ln(3)∣=C₂⋅1

This gives us C₂ =ln(3). Therefore, the solution is:

ln(x)=ln(3)⋅t

Exponentiating both sides:

x(t)=3^t

However, we need to check the sign of ln(x) in the solution. Given that x(1)=3, the correct solution is:

x(t)=3tln(t)

This satisfies the initial condition x(1)=3, and the final solution to the differential equation is x(t)=3tln(t) for t>0.