Question

A cylindrical bar of metal having a diameter of 15.7 mm and a length of 178 mm is deformed elastically in tension with a force of 49100 N. Given that the elastic modulus and Poisson's ratio of the metal are 67.1 GPa and 0.34 respectively, Determine the following:(a) The amount by which this specimen will elongate (in mm) in the direction of the applied stress. The entry field with incorrect answer now contains modified data.(b) The change in diameter of the specimen (in mm). Indicate an increase in diameter with a positive number and a decrease with a negative number.

Answer 1

0.6727

-0.02017

Step-by-step explanation:

diameter = 15.7

l = 178

E =elastic modulus = 67.1 Gpa

poisson ratio = 0.34

p = force = 49100N

first we calculate the area of the cross section

`A=(\pi )/(4) d^(2)`

`A=(\pi )/(4) (15.7)^(2) \\A = (774.683)/(4) \\`

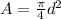
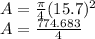
A = 193.6mm²

1. Change in directon of the applied stress

`= (pl)/(AE)`

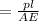
= 49100*178/193.6*67.1*10³

=
`=(8739800)/(12990560)`

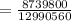
δl = 0.6727 mm

2. change in diameter of the specimen

equation for poisson distribution =

m = -(δd/d) / (δl/l)

0.34 = (δd/15.7) / (0.6727/178)

0.34 = (-δd * 178) / 15.7 * 0.6727

0.34 = -178δd / 10.56139

we cross multiply

10.56139*0.34 =-178δd

3.5908726 = -178δd

δd = 3.5908726/-178

δd = -0.02017 mm

the change in dimeter has a negative sign. it decreases