Question

Find three non-negative numbers a, b, and c such that their product is a maximum when the numbers a, b, and c are constrained by the relation 6a + b + c = 10.

Answer 1

The maximum product occurs when
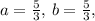`\(a = (5)/(3)\), \(b = (5)/(3)\),` and
`\(c = (5)/(3)\), yielding \(P_{\text{max}} = \left((5)/(3)\right)^3\).`

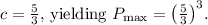
To find three non-negative numbers a, b, and c such that their product is maximized under the constraint
`\(6a + b + c = 10\)`, we can use the AM-GM (Arithmetic Mean-Geometric Mean) inequality.

Step 1: Formulating the Objective Function

Let P = abc be the product we want to maximize.

Step 2: Expressing the Constraint as an Equality

The constraint 6a + b + c = 10 is equivalent to 6a = 10 - b - c, allowing us to substitute 6a in the expression for P.

Step 3: Applying AM-GM Inequality

Apply the AM-GM inequality to 10 - b - c, b, c:

`\[ ((10 - b - c) + b + c)/(3) \geq \sqrt[3]{(10 - b - c)bc} \]`

Simplify the expression, and rearrange to isolate the product P.

Step 4: Finding the Critical Points

Find the critical points of P by solving for equality in the AM-GM inequality, considering the non-negativity constraint.

Step 5: Analyzing Endpoints

Check the values of P at the endpoints of the feasible region, where a, b, and c are non-negative.

The maximum product occurs when
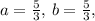`\(a = (5)/(3)\), \(b = (5)/(3)\),` and
`\(c = (5)/(3)\), yielding \(P_{\text{max}} = \left((5)/(3)\right)^3\).`

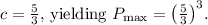
This solution is derived using the AM-GM inequality and ensures the equality constraint is satisfied, resulting in the maximum possible product.